Tessellations

A tessellation of a plane is the filling of the plane with repetitions of figures in such a way that no figures overlap and there are no gaps

Tessellations can be drawn by sliding, flipping, and turning certain polygons

Here are some different types of tessellations:

Regular Tessellations

Semi-regular Tessellations

Here's a short video that summarizes how to make a tessellation!

This website offers a wide variety of internet based tessellation games and activities!
http://mathwire.com/geometry/tess.html

Translations, Rotations, Reflections, and Glide

Translations or slide
Moves every point of the plane to a specific distance in a specified direction along a straight line
Image of A = A'

Rotations or turn
Congruent figures that result from a rotation about a point.  A rotation is a transformation of a plane determined  by holding one point -the center- fixed and rotating the plane about this point by a certain amount in a certain direction (a certain number of degrees either clockwise or counterclockwise)

(A 360 degrees rotation is called identity transformation)

Reflections or flip
A reflection reverses the orientation of the original figure

Glide Reflection
 A glide reflection is a transformation consisting of a translation followed by a reflection in a line parallel to the slide arrow

This website has a really fun interactive game to help kids learn about transformations!
http://www.kidsmathgamesonline.com/geometry/transformation.html

This site offers several interactive transformations games to try out!

http://www.onlinemathlearning.com/transformation-games.html

Symmetries

Line Symmetries:
A geometric figure has a line of symmetry if it is its own image under a reflection

Here are some things in real life that have line symmetry:

Rotational (Turn) Symmetries:
A.  A figure has rotational symmetry, or turn symmetry, when the traced figure can be rotated less than 360 degrees about some point so that it matches the original figure

B  When a figure will coincide with itself after a rotation a degree amount is stated.  Here is a video to further demonstrate rotational symmetry

Point Symmetry:
Any figure that has 180 degrees rotational symmetry is said to have point symmetry about the turn center.  Any figure with point symmetry is its own image under a half-turn

This website has a great line symmetry game for younger kids!
http://www.innovationslearning.co.uk/subjects/maths/activities/year3/symmetry/shape_game.asp

Surface Areas

Surface area measurement is used in everyday life: carpeting, painting your house, buying roofing, seal-coating driveways, etc...

 Surface area of a right prism:

•  Net - cut and lay prism flat
•  Net for a cube = 6 X Edges squared
•  Sum of areas of lateral faces is the lateral surface area
•  Surface area is the sum of the lateral surface area and the area of the bases

Surface area of a cylinder

Surface area of a pyramid 

Surface Area = n(1/2 x B x L) + B

Surface area of a cone

Surface area of a sphere

Here is an awesome website with interactive Surface Area activities to practice with!
http://www.brainingcamp.com/resources/math/surface-area/
 

Hello there! The purpose of this blog is to teach a little about geometry and offer some websites for teachers and future teachers to use.  My name is Peter Elliot.  I am an education major at Mesa Community College. Here is a little background info on me: I was born in Illinois, just outside of Chicago and moved to Texas when I was 10 years old. After living there for four years I relocated once more to Arizona and have lived there ever since. I have always loved working with children and had plenty of experience when I was younger from babysitting and teaching Sunday School.  Another passion in my life is music. I love to sing and have a very eclectic taste in music ranging from classical to 70s/80s heavy metal. When I can find the time I plan on taking some actual singing and guitar lessons. Music is definitely something I will be using as a teacher!  I do not currently have a special someone in my life but I am currently enjoying being single while I focus on starting a career.  I cannot wait to become a teacher and start shaping the minds of tomorrow!!

The Pythagorean Theorem

Pythagorean Theorem- If a right triangle has legs of lengths a and b and hypotenuse of length; then:

 

In a triangle. the side opposite the right angle is the hypotenuse.  The other two sides are legs.  The Pythagorean Theorem states that the are of square with the hypotenuse of a right triangle as a side is equal to the sum of the areas of the square with the legs as sides.

Here is a fun video to go more in depth with the Pythagorean Theorem!

 

Another theorem for calculating area is called Pick's Theorem:

B = Border Points
I = Interior Points

To learn more about Pick's Theorem, check out this informative video!

These websites have some great examples and ideas to use to teach these two theorems!

http://www.mathsisfun.com/pythagoras.html
http://illuminations.nctm.org/LessonDetail.aspx?ID=L623

Area of Polygons

Area- measured using square units.  The area of a region is the number of nonoverlapping square units that cover the region.  A square foot has 1 foot on each side, denoted as 1 ft squared.

I.  Area on Geoboard

Addition Method- finding the sum of the smaller areas
Rectangle Method- construct a rectangle around the shape then subtract the shaded part


II.  Converting Units of Area

III.  Area of Rectangle

Area = length x width

IV.  Area of a Parallelogram

Area = base x height

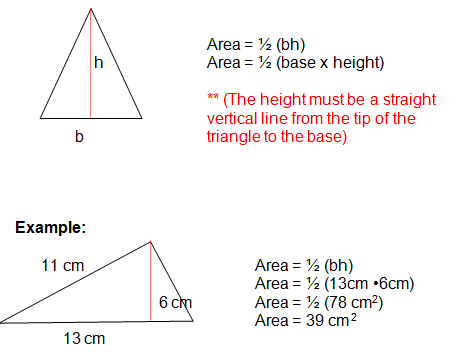
V.  Area of a Triangle

Area = 1/2 x b x h or (b x h)/2

VI.  Area of Trapezoid

Area = 1/2 x (base1 + base2) x height

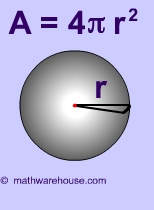
VII.  Area of Circle

Just for fun here is a very awesome way to remember to remember  the formulas for the area of a circle and the circumference!


Cheery Pie Delicious
 C = pi x diameter

Apple Pies Are Too